
𝒆π𝒊 + 1 = 0
이중 𝒆는 신비의 수로 약간의 설명이 필요하다. 예를 들어 돈을 연 100%의 이자로 1년간 단리(單利)로 맡기면 원금의 2배가 된다. 6개월 후 이자 정산을 하고 다시 6개월을 맡기면 (1+1/2)²=2.25배가 된다. 또 월 단위 복리(複利), 즉 매월 말에 이자 정산을 하며 1년을 맡기면 (1+1/12)¹²=2.613····, 원금의 약 2.6배가 될 것이다.
이 단위 기간을 한 달이 아니라 하루로 하면 2.714····이 된다. 이 기간을 1초 단위 혹은 무한소로 하면 이 수는 무리수인 2.7182818285····로 수렴하는데, 이 수를 자연상수 𝒆라 부른다. 자연상수 𝒆는 성장과 감소, 확률·통계, 금융, 해석학 등에 등장하는 ‘자연의 언어’ 같은 수로 미적분과 로그함수에서 아주 긴요하게 쓰인다.
오일러 공식을 설명할 수 없으면서도 여기에 소개하는 것은, 보는 것만으로도 이 식이 너무 아름답기 때문이다. 한 줄 안에 수학의 핵심이라고 불리는 다섯 개의 숫자가 항등식으로 묶여 있으니 말이다. 도대체 자연상수 𝒆를 원주율 π와 상상 속의 허수인 𝒊 제곱하면 –1이 나온다는 것을 상상할 수 없다.
이 식을 자세히 알고 싶은 분은 데이비드 스티프가 쓰고 김수환이 번역한 <신의 방정식 오일러 공식>을 읽어 보기를 권한다. 알기 쉽게 자세히 설명되어 있어 웬만하면 이해할 수 있다.
오일러는 또 모든 다면체의 꼭짓점 수(V)에 면의 수(F)를 더하면 변의 수(E)보다 2가 더 많다는 것을 증명했다. 예를 들어 직육면체의 꼭짓점은 8개, 면은 6개, 변의 수는 12개이므로 8+6–12=2이다. V+F–E=2로 표시되는 이 식을 오일러 정리(Euler’s theorem)이라 부른다.
이 정리는 난제로 알려졌던 쾨니히스베르크 다리 건너기 문제를 오일러가 푸는 과정에서 알아냈다고 한다. 어떤 도형을 손을 떼지 않고 한 번에 그릴 수 있는지 알아보는, 소위 ‘한 붓 그리기 놀이’와 비슷한 문제다.
오일러가 살았던 프로이센 왕국 쾨니히스베르크시 프레겔강에는 두 섬이 있고, 이 섬들과 양안(兩岸)을 잇는 7개의 다리가 있다. 그 다리들을 한 번씩만 건너 일곱 개 다리를 모두 건널 수 있는가 하는 문제가 오랫동안 많은 수학자를 괴롭혔다. 직접 해 보려고 동선을 아무리 그려보아도 다리 하나가 건너지 못한 채로 남았는데, 왜 그런지 아무도 설명하지 못했다.
결국 1735년 오일러가 다음 그림을 포함한 논문을 발표하면서 이 문제를 해결했다. 오일러는 두 섬과 양안을 A, B, C, D로 표시하고, 다리 일곱 개를 a부터 g까지 선으로 표시한 스케치를 그려 문제를 간단하게 만들었다. 즉 A~D를 꼭짓점(node), a~g를 연결선(line)으로 삼은 도형으로 풀이한 것이다.
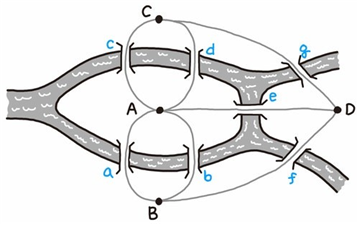
논문에 포함된 이 스케치는 현대에 이르러 위상수학(位相數學)에 쓰이는 그래프 구조의 원형이 되었다. 위상수학이란 도형이나 공간을 늘리거나 줄여도 변하지 않는 성질을 연구하는 수학의 한 분야로, 거리나 크기 같은 양적 관계를 무시하고 도형의 연결, 근접성, 연속성 등 관계적 위치를 중시한다. 오늘날 지하철 노선도가 대표적인 예라 할 수 있다.
오일러는 각 꼭짓점에 모이는 연결선의 수에 주목했다. 이 문제에서는 A에는 5개, B·C·D에는 각각 3개의 연결선이 모이는데, 이들은 모두 홀수다. 오일러는 연결선이 홀수인 꼭짓점이 세 개 이상이면 모든 다리를 한 번씩만 건너는 것은 불가능하다는 것을 증명하였다.
연결선이 짝수일 경우는 ‘나감–들어옴’으로 되돌아올 수 있지만, 홀수인 경우는 마지막 하나가 나가면 돌아올 수 없고, 들어오면 나갈 수 없다. 홀수 연결선을 가진 꼭짓점이 두 개면 하나는 출발점, 하나는 도착점으로 삼을 수 있지만, 세 번째까지는 갈 수 없다. 이 문제의 경우 홀수 연결선을 가진 꼭짓점이 A~D 네 개이므로 절대로 모든 연결선을 거칠 수 없다.
레온하르트 파울 오일러(1707~1783)는 스위스 태생의 수학자, 물리학자, 천문학자, 지리학자, 논리학자, 공학자로 유클리드, 아르키메데스, 뉴턴, 가우스 등과 함께 인류 역사상 최고의 수학 천재로 평가받는다. 스위스 바젤 출신이지만 러시아에서 30여 년, 독일에서 25년 동안 연구에 매진했다.
허수의 기본이 되는 √–1에 𝒊라는 기호를, 자연상수에 𝒆라는 기호를 붙인 것도 오일러다. 오일러는 지나치게 연구에 몰두한 나머지 50대 말에 두 눈 모두 실명했는데, 그 후에도 17년 동안 맹렬한 연구 실적을 쌓아 자신의 전체 업적 중 절반 이상을 이 기간에 이루었다.
그는 시력을 잃은 것에 대해 “마음을 산만하게 하던 것이 하나 줄었다”라고 쾌활하게 말했다고 한다. 그는 그 이외에도 여러 가지 좌절과 비극을 겪었지만, 낙천적 성격으로 이를 극복하였다. 그는 천재들이 흔히 보이는 것처럼 성격이 강퍅하거나 거만하지 않고, 누구에게나 따뜻하고 겸손하게 대했다고 한다.
오일러야말로 진정 ‘먼저 사람이 되기’를 실천한 사람이다.



